🎨 Nonlinear Art Gallery
🔬✨ Nonlinear systems are mesmerizing mathematical structures that give rise to intricate patterns, chaotic beauty, and emergent complexity. This gallery is a carefully curated collection of “mathematical pieces of art” — some derived from my own research, others widely recognized in the scientific literature.
💡✨ While these visualizations are rooted in rigorous mathematics and computational models, their artistic appeal transcends science. Each image captures the elegance of fractals, attractors, wave interactions, and bifurcations, revealing the hidden beauty of complex systems.
🔍✨ Explore, zoom in, and immerse yourself in the wonders of nonlinear mathematics. Whether you’re a scientist, an artist, or simply an admirer of beauty, I invite you to see how math becomes art. Discover the elegance of chaos. Witness order emerging from randomness.
🖼️ Enjoy the gallery!
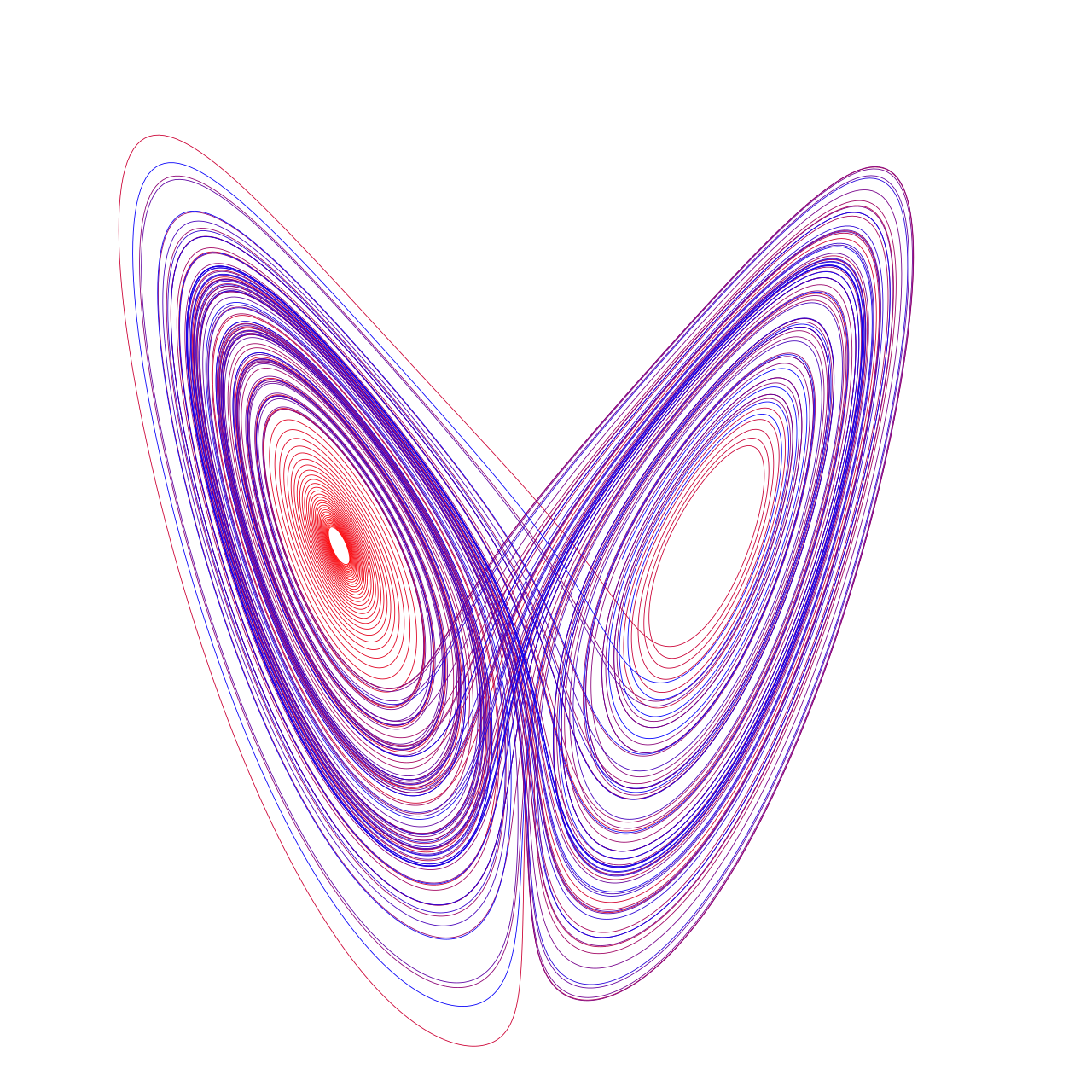 | Lorenz Attractor - A 3D chaotic system with butterfly-shaped trajectories, representing the sensitive dependence on initial conditions. 📖 Reference: Lorenz, Edward Norton (1963). Deterministic nonperiodic flow. Journal of the Atmospheric Sciences. 20 (2): 130–141 🔗 Read More Here |
 | Standard Map - An area-preserving chaotic map from a square with side 2π onto itselt 📖 Reference: B.V.Chirikov, Research concerning the theory of nonlinear resonance and stochasticity, Preprint N 267, Institute of Nuclear Physics, Novosibirsk (1969) 🔗 Read More Here |
 | |
 | |
 | |
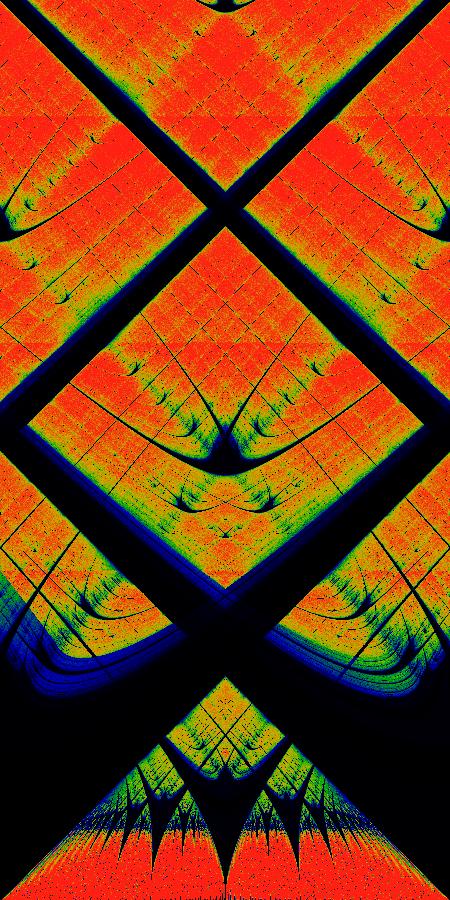
 | Circle Map - A mathematical model used to study phase locking in coupled oscillators and chaotic behavior in nonlinear systems. 📖 Reference: Glass, L.; Perez, R. (1982). Fine structure of phase locking. Physical Review Letters. 48 (26): 1772. 🔗 Read More Here |
 | |
 | |
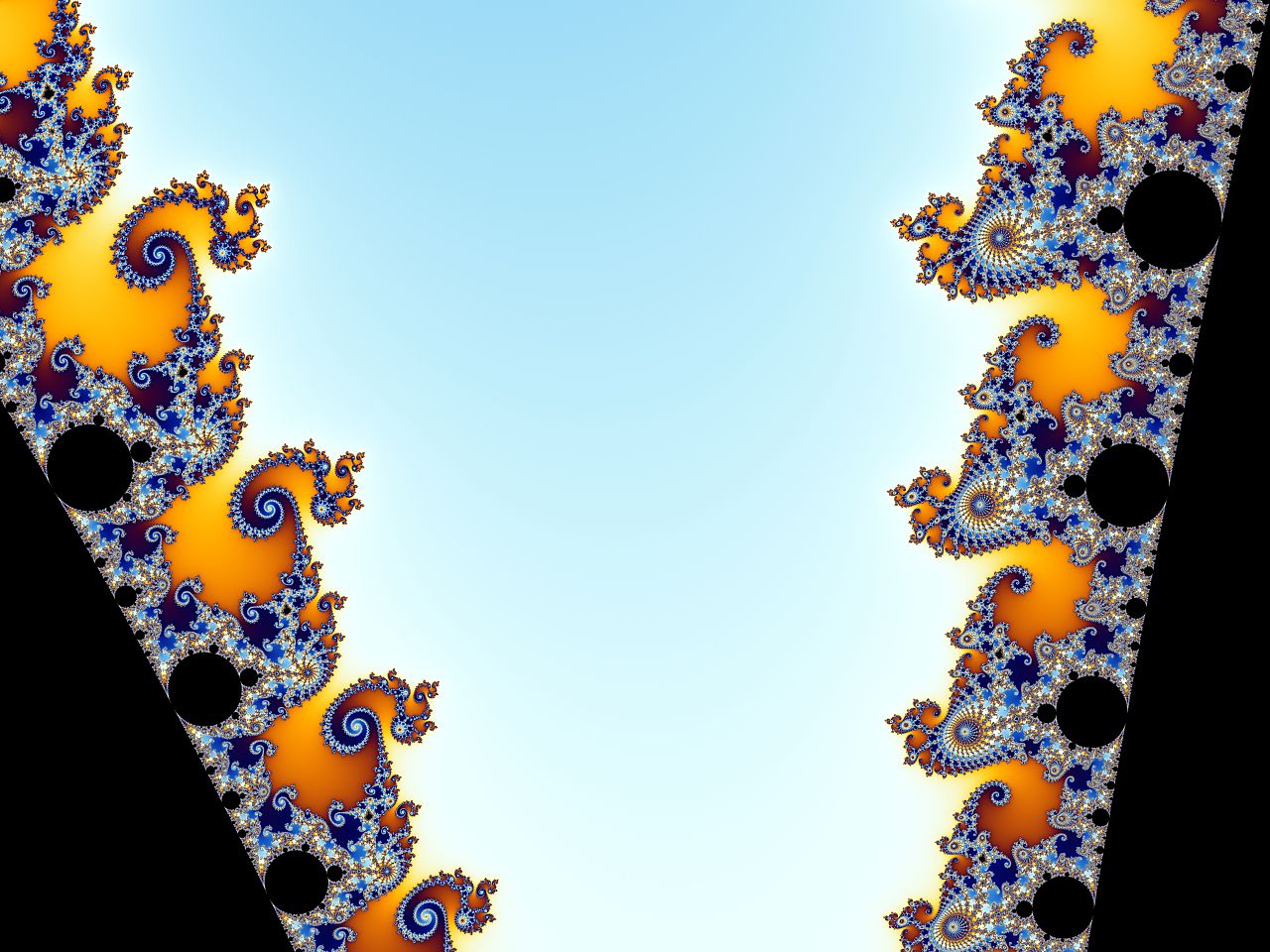
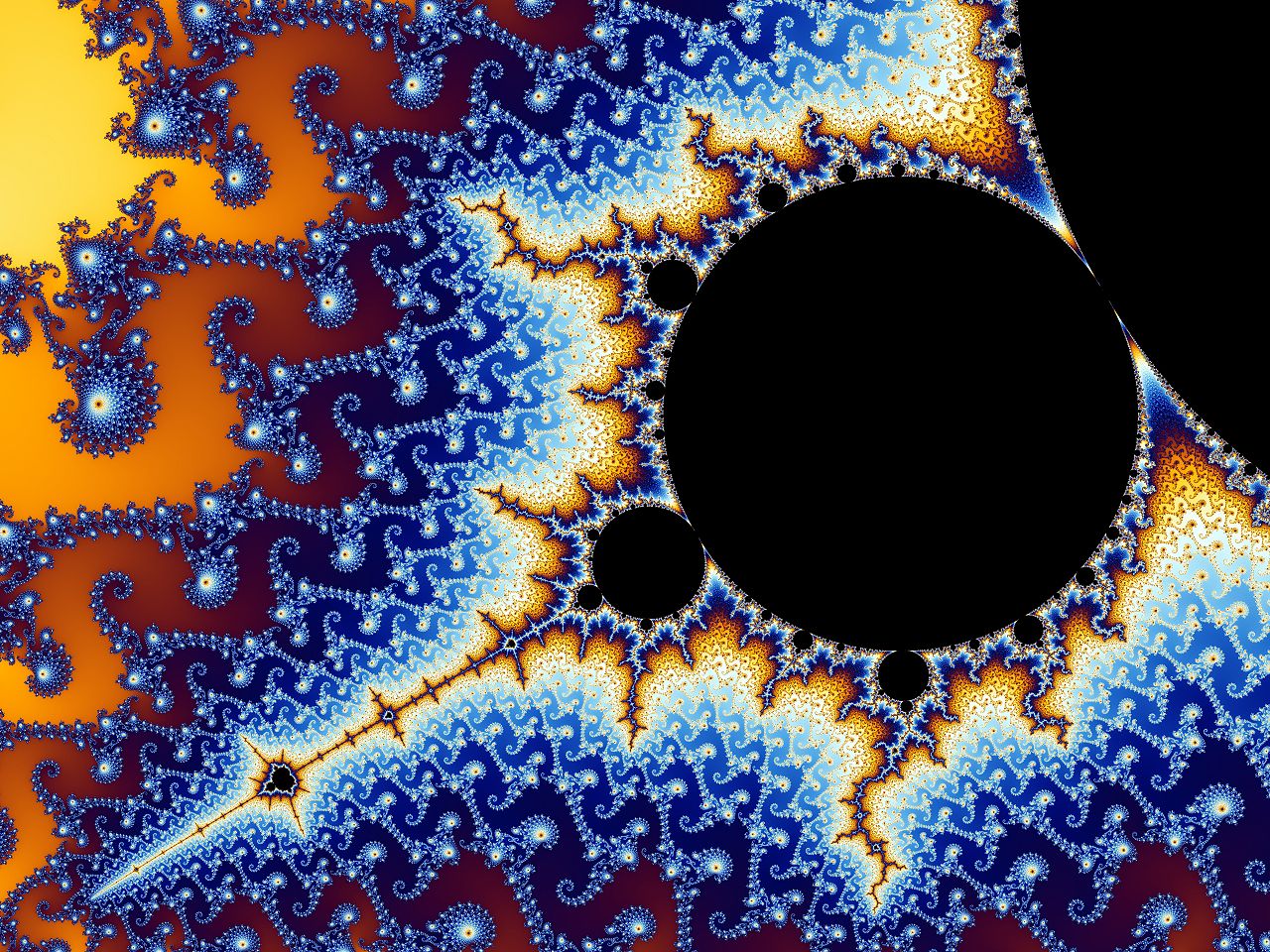
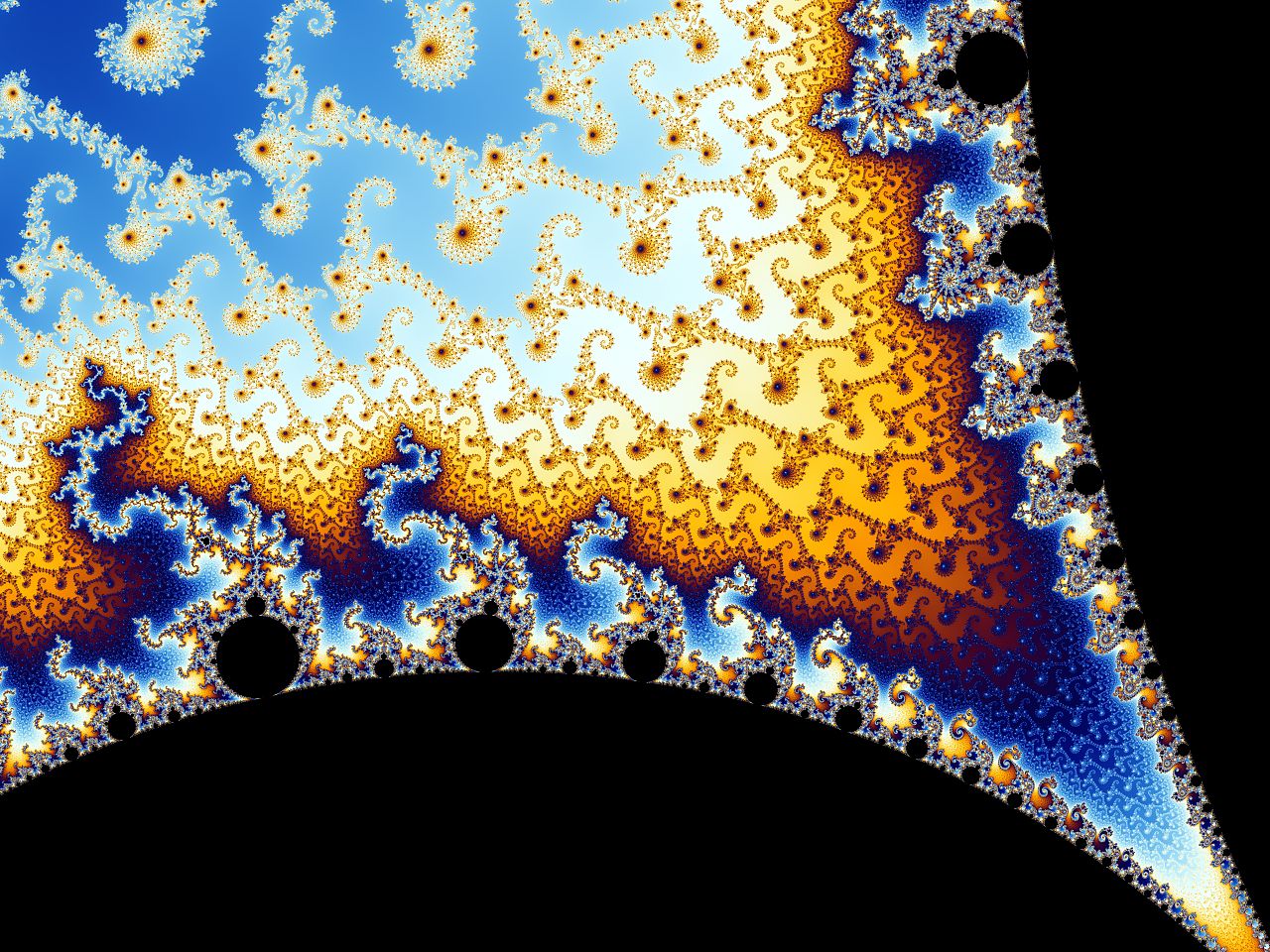
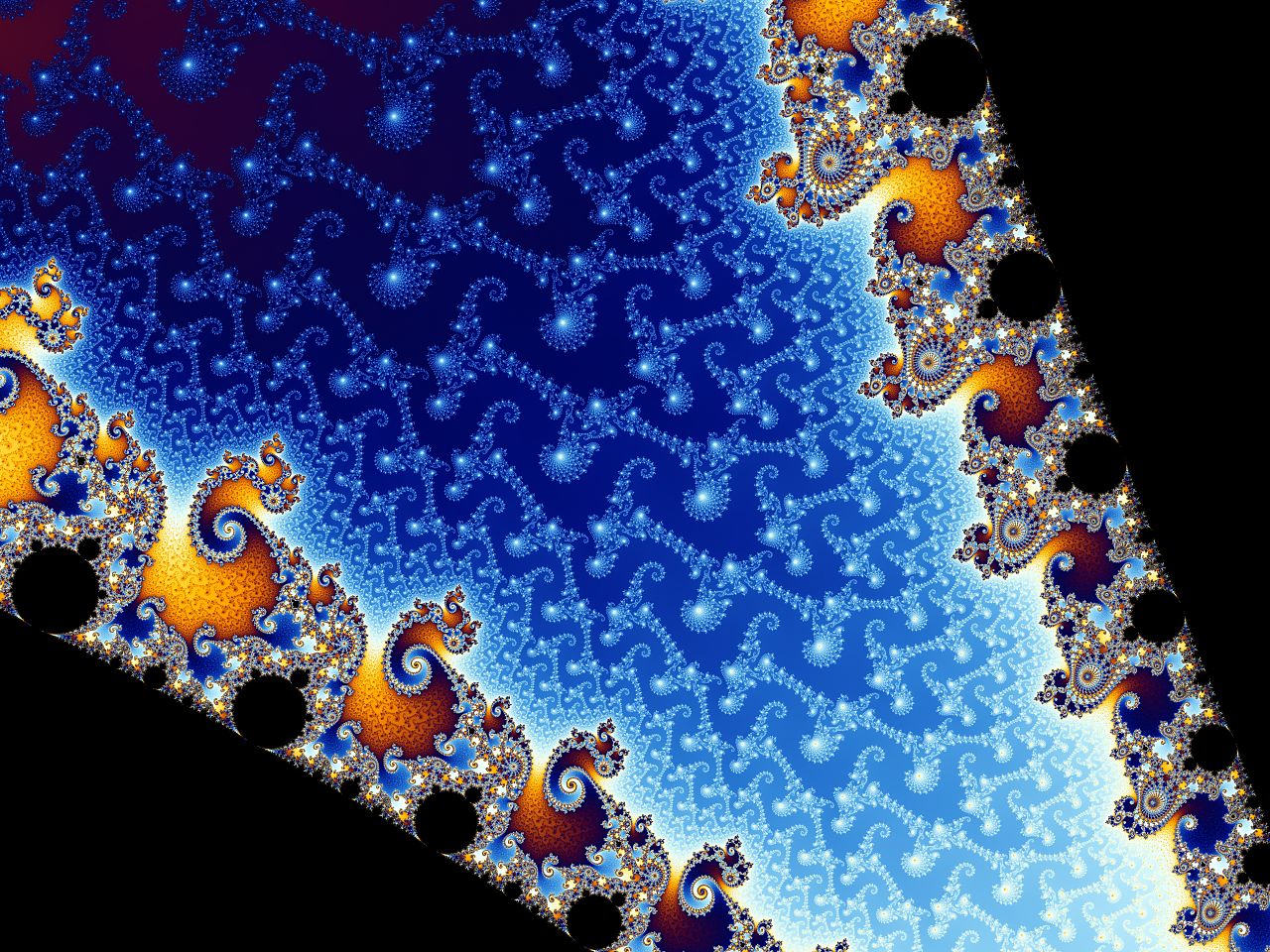
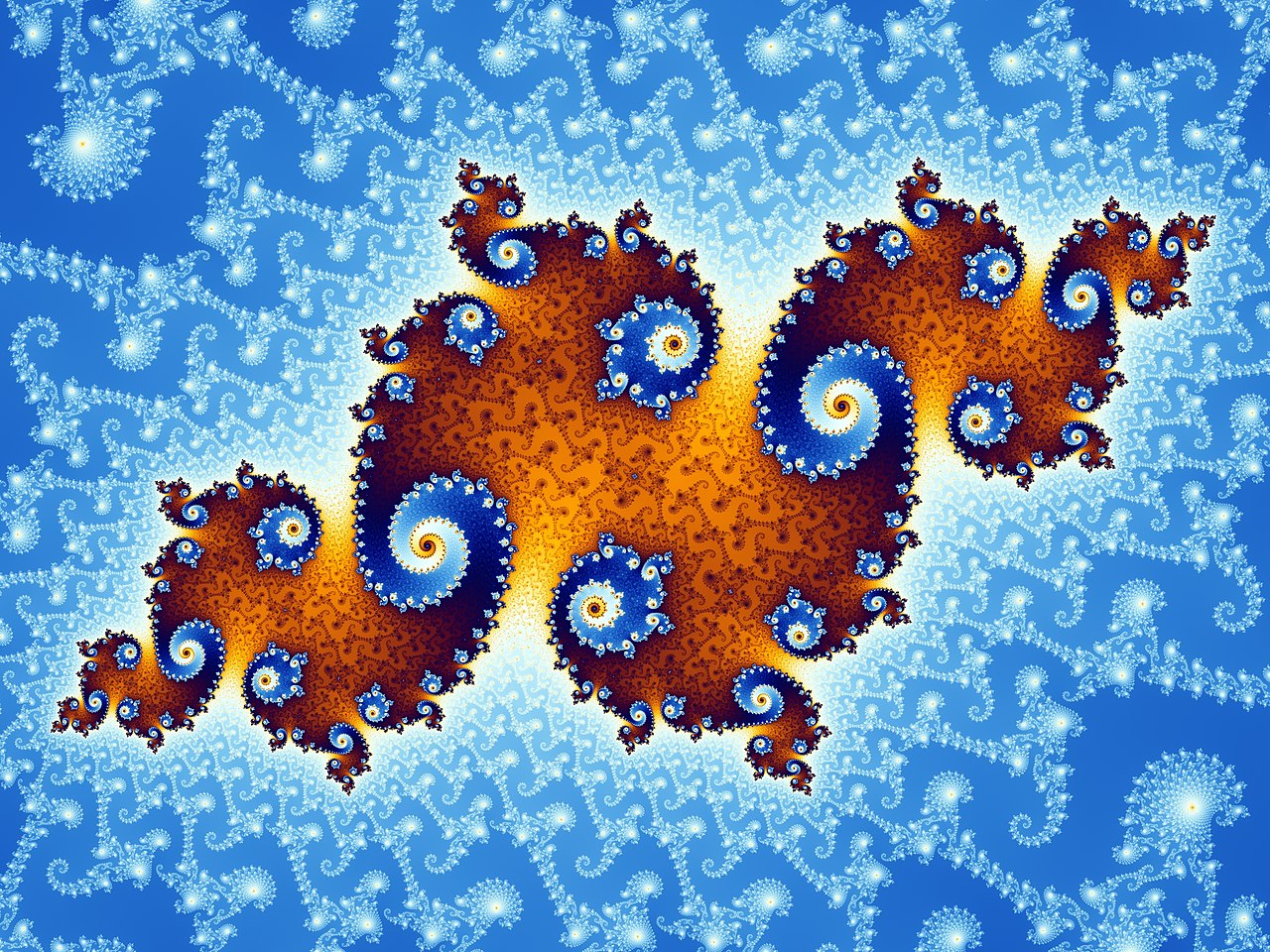
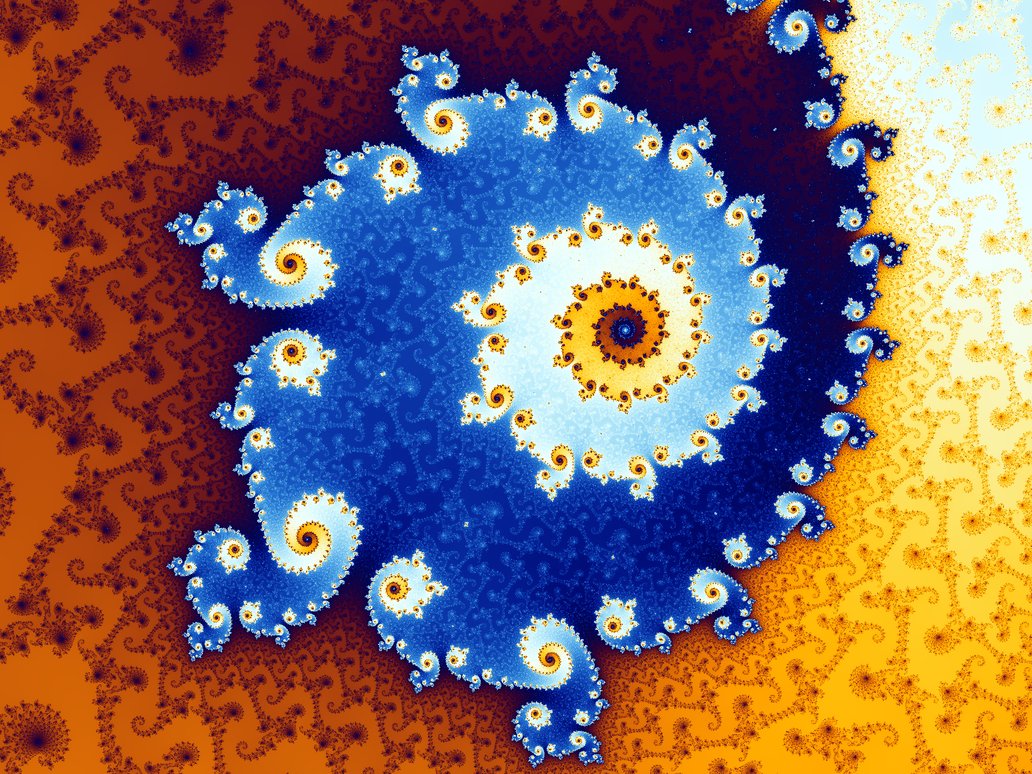
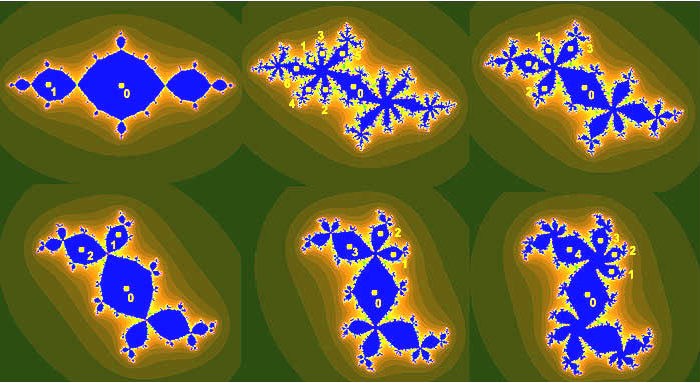
 | Mandelbrot Set - The Mandelbrot Set is a famous fractal defined by the simple recurrence relation z_{n+1} = z_n^2 + c, where complex numbers generate infinitely intricate boundary patterns. It is a cornerstone of chaos theory and fractal geometry. 📖 Reference: Robert Brooks and Peter Matelski, The dynamics of 2-generator subgroups of PSL(2,C), in Irwin Kra (1981). Irwin Kra (ed.). Riemann Surfaces and Related Topics: Proceedings of the 1978 Stony Brook Conference 🔗 Read More Here |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
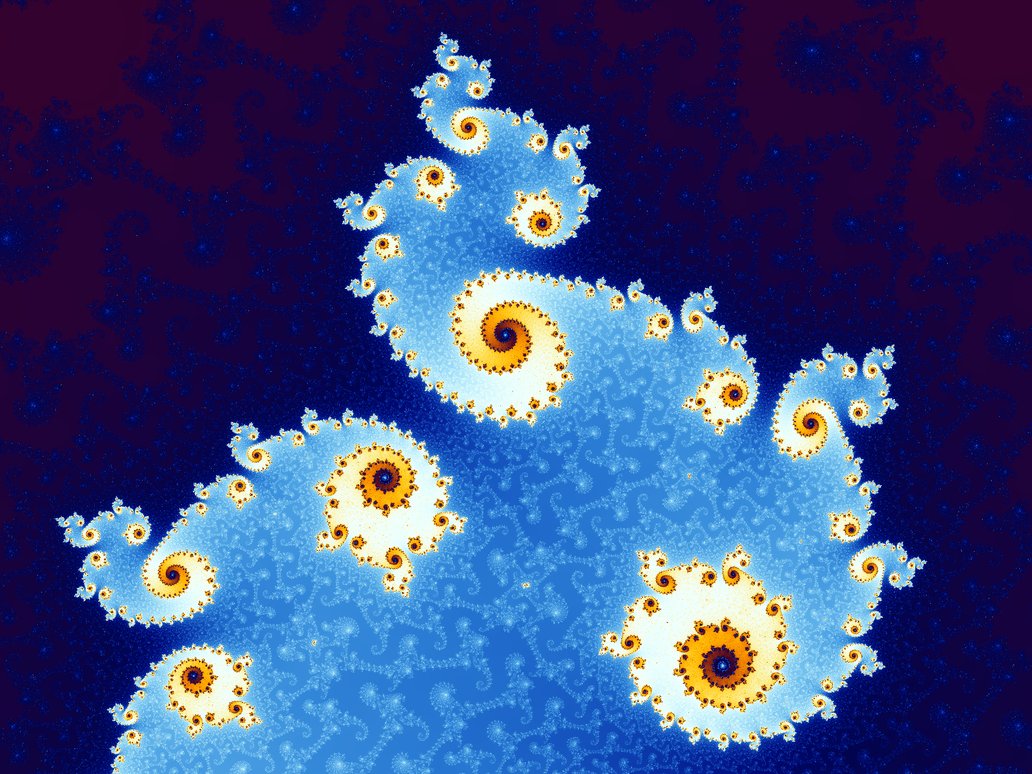 | |
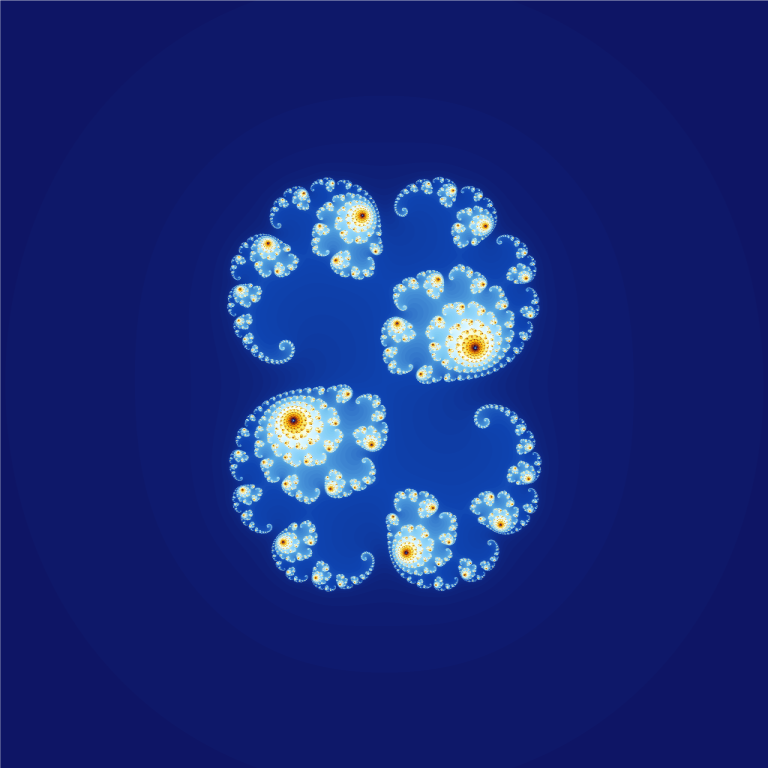
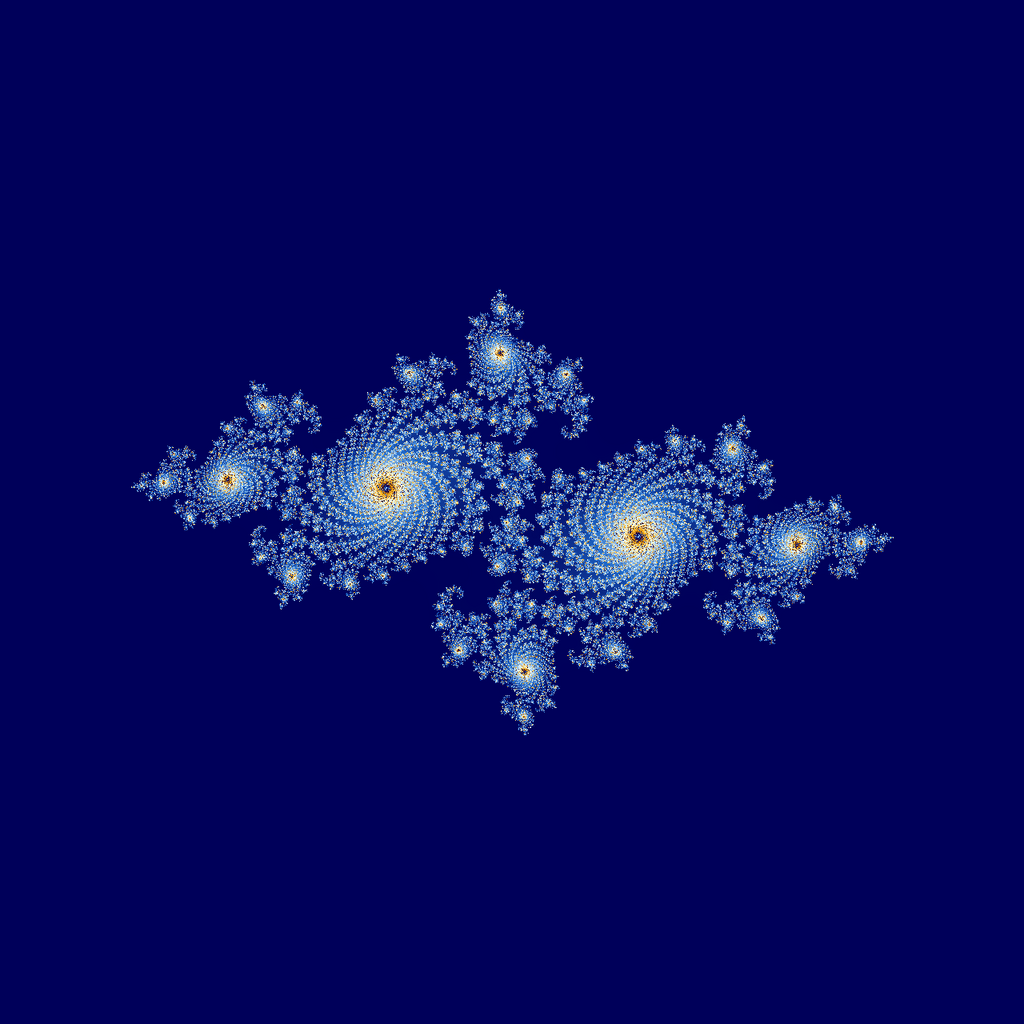
 | Julia Sets - Julia Sets are fractal structures closely related to the Mandelbrot Set. They are generated using the iteration z_{n+1} = z_n^2 + c, varying the complex parameter c. The boundary of the set exhibits intricate self-similar structures, making it a key object in dynamical systems. 📖 Reference: Gaston Julia (1918) Mémoire sur l'iteration des fonctions rationnelles, Journal de Mathématiques Pures et Appliquées, vol. 8, pages 47–245. 🔗 Read More Here |
 | |
 | |
 | |
 | |
 | |
 | Gauss Iterated Map - A nonlinear iterated map of the reals into a real interval given by the Gaussian function. 📖 Reference: M. Tosin, M. V. Issa, D. Matos, A. Nascimento, A. Cunha Jr. Employing 0-1 test for chaos to characterize the chaotic dynamics of a generalized Gauss iterated map. XIV Conferência Brasileira de Dinâmica, Controle e Aplicações (DINCON 2019), 2019, São Carlos, Brazil. 🔗 Read More Here |
 | Bistable Vibration Energy Harvester - A nonlinear iterated map of the reals into a real interval given by the Gaussian function. 📖 Reference: J. P. Norenberg, R. Luo, V. G. Lopes, J. V. L.L. Peterson, A. Cunha Jr, Nonlinear dynamics of asymmetric bistable energy harvesters, International Journal of Mechanical Sciences, vol. 257, pp. 108542, 2023. 🔗 Read More Here |
